Spectral Properties of Generalized Correlation Matrices
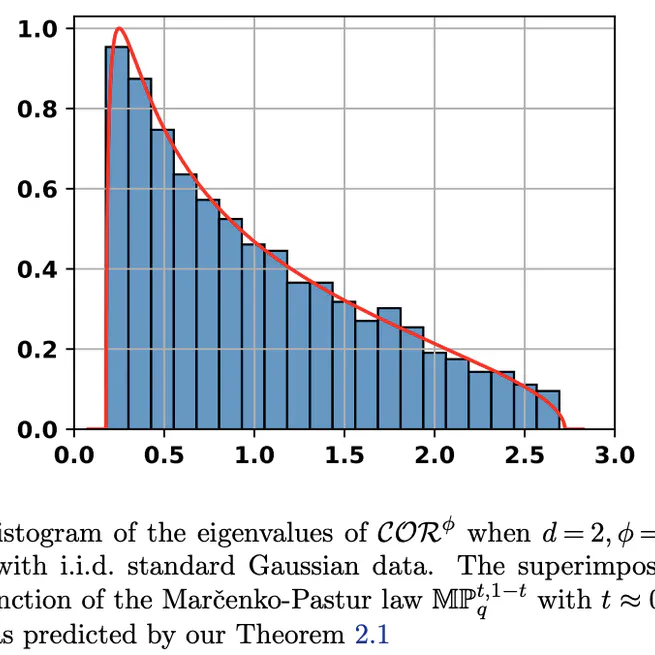
We introduce a family of coefficients that generalize the notion of correlation and explore their properties in the large dimensional multivariate case, showing that in the null case of uncorrelated variables, the spectrum of generalized correlation matrices is distributed according to an affine transformation of the Marčenko-Pastur law.
Sep 29, 2025
Another Marčenko-Pastur law for Kendall's tau
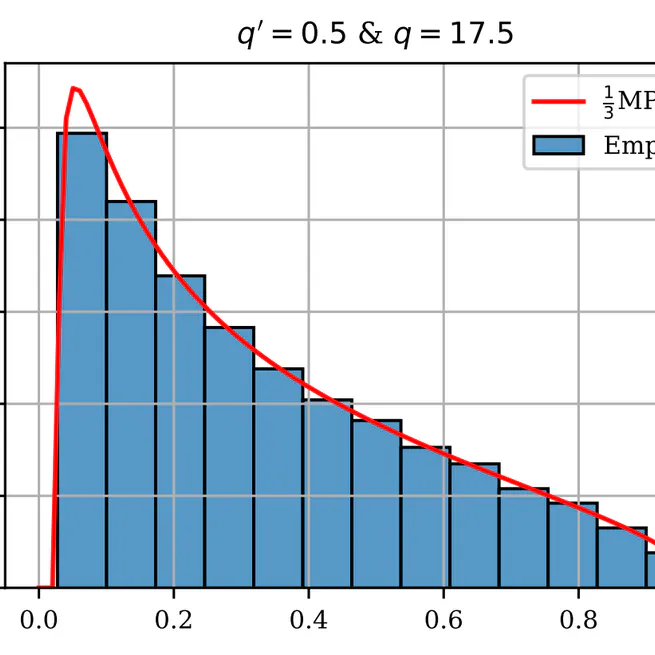
Bandeira *et al.* (2017) show that the eigenvalues of the Kendall correlation matrix of n i.i.d. random vectors in ℝᵖ are asymptotically distributed like 1/3 + (2/3)·Y₍q₎, where Y₍q₎ has a Marčenko–Pastur law with parameter q = lim(p/n) if p, n → ∞ proportionately to one another. Here we show that another Marčenko–Pastur law emerges in the \"ultra-high dimensional\" scaling limit where p ∼ q′·n²⁄2 for some q′ > 0. In this quadratic scaling regime, Kendall correlation eigenvalues converge weakly almost surely to (1/3)·Y₍q′₎.
Mar 1, 2025