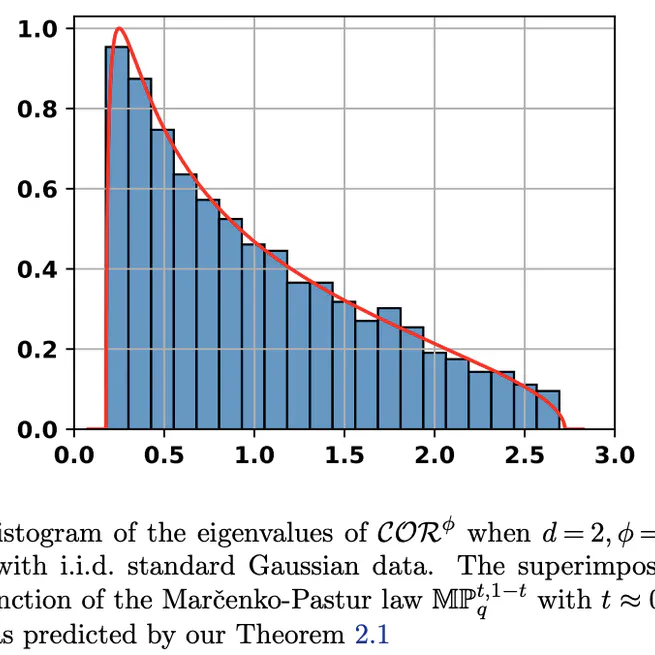
We introduce a family of coefficients that generalize the notion of correlation and explore their properties in the large dimensional multivariate case, showing that in the null case of uncorrelated variables, the spectrum of generalized correlation matrices is distributed according to an affine transformation of the Marčenko-Pastur law.
Sep 29, 2025
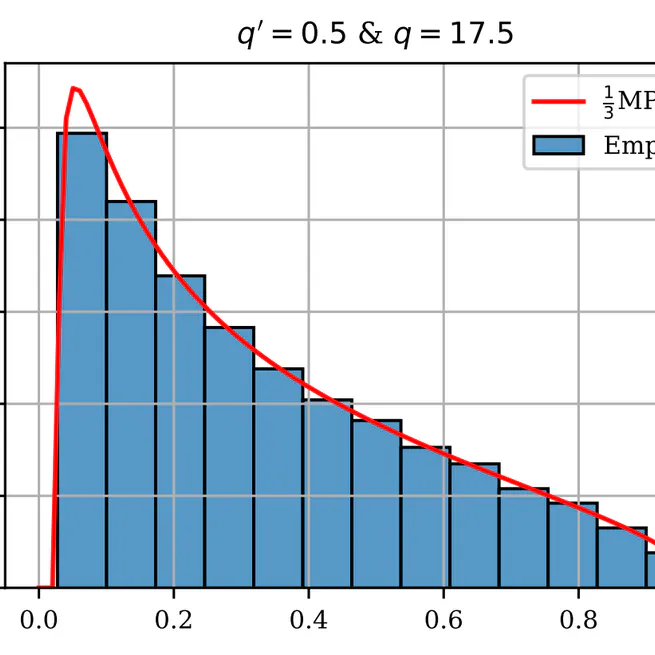
Bandeira *et al.* (2017) show that the eigenvalues of the Kendall correlation matrix of n i.i.d. random vectors in ℝᵖ are asymptotically distributed like 1/3 + (2/3)·Y₍q₎, where Y₍q₎ has a Marčenko–Pastur law with parameter q = lim(p/n) if p, n → ∞ proportionately to one another. Here we show that another Marčenko–Pastur law emerges in the \"ultra-high dimensional\" scaling limit where p ∼ q′·n²⁄2 for some q′ > 0. In this quadratic scaling regime, Kendall correlation eigenvalues converge weakly almost surely to (1/3)·Y₍q′₎.
Mar 1, 2025
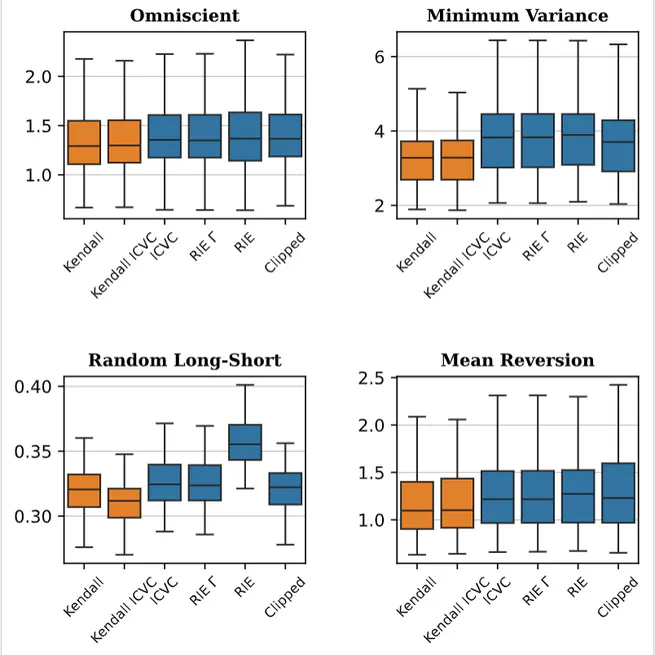
Markowitz's optimal portfolio relies on the accurate estimation of correlations between asset returns, a difficult problem when the number of observations is not much larger than the number of assets. Using powerful results from random matrix theory, several schemes have been developed to "clean" the eigenvalues of empirical correlation matrices. By contrast, the (in practice equally important) problem of correctly estimating the eigenvectors of the correlation matrix has received comparatively little attention. Here we discuss a class of correlation estimators generalizing Kendall's rank correlation coefficient which improve the estimation of both eigenvalues and eigenvectors in data-poor regimes. Using both synthetic and real financial data, we show that these generalized correlation coefficients yield Markowitz portfolios with lower out-of-sample risk than those obtained with rotationally invariant estimators. Central to these results is a property shared by all Kendall-like estimators but not with classical correlation coefficients zero eigenvalues only appear when the number of assets becomes proportional to the square of the number of data points.
Oct 1, 2024